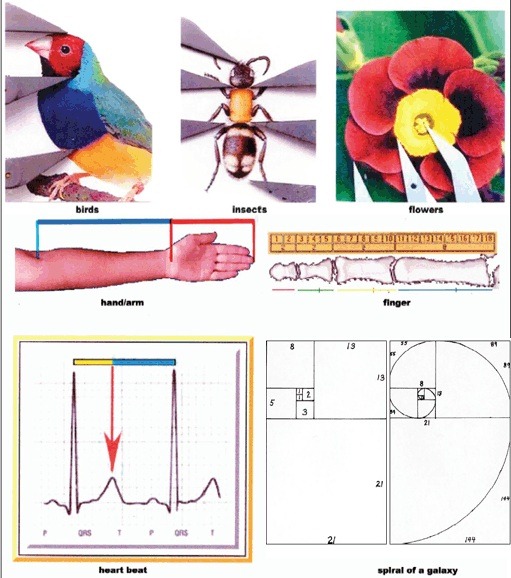
النسبة الذهبية _فاي_ الرقم الغريب و أسرار الطبيعة ..
و قد اعتمد على النسبة الذهبية في رسم لوحته الشهيرة المسماه The Vitruvian Man أو الرجل الفيتروفي و التي تعتبر من أفضل لوحاته
ما هى الطريقة لحساب النسبة الذهبية بالتصاميم ؟النسبة الذهبية أو Goldin raito يوجد لها طريقتين الاولي خطية والثانية محورية أو تكون على شكل حلزوني لتقريب الوصف
كلا الطريقتين تعتمد على النسبة على1.6 في الفرق بين طولين أو تزايد رقمي على شكل0،1،1،3،5،8،13،21،34،55
في المعمار في التصميم أو الرسم أو التصوير، نستخدم النسبة الذهبية لتحديد أفضل مكان لوضع جسم أو أفضل توزيع للمساحة أو أفضل موقع للمداخل أو المخارج، أو في التصوير أفضل موقع لوجود الجسم المراد أبرازه في الصورة وفي الرسم كذلك. وكذلك في أختيار الدرجة المناسبة للألوان أستخدم النسبة الذهبية لتحديد زوجين من الألوان لتجانس أفضل.
أذا كنت تقصد كيف نحسب النسبة الذهبية فقط فان في الطريقة الخطية ولنفترض أن لدينا خط طولة10 متر فأنك تقسم هذا الطول على1.6 ليعطيك6.25 هذا الرقم هو بعد النقطة بالنسبة الذهبية من طرفي الخط مثل النقطة التي تقع على بعد6.25 عن يمين الخط والتي تقع أيضا على بعد3.75 على يسار الخط.
حساب النسبة الذهبية الحلزونية أو اللولبية وهي تستخدم للمساحة فلنفرض أن لديك مساحة مستطيلة8 سم *13 سم لو قسمنا هذه المساحة على خطوط لكل واحد سم ونستخدم الرقم1.6 كما أستعملناه لتقسيم الخط بالمثال في الأعلي لتقسيم أضلاع المستطيل لتقسيم المساحة، الضلع الأول13 تقسيم1.6 يعطينا8.125 بطرحها من13 يعطينا4.875 نرسم خط مستقيم يمر بهذه النقطة ويتقاطع بالضلع الموازي له، وهكذا لباقي الأضلاع على جميع المحاور. ثم بعد ذلك نرسم شكل حلزوني يمر بداخل المربعات ويلمس أضلاعها من الداخل (ضلعين).
هذا بالنسبة لطريقة حساب النسبة الذهبية، بالنسبة لأستخدامها فأنه فقط يتم أستعمالها كدليل لتحديد أهم أو أفضل نقاط في التصميم (نقاط القوة) وهذه كانت نظرية للعالم الأيطالي فابوناتشي استنبطها من وجود هذا التركيب والتشكيل في الطبيعة، بسبب هذا قال العالم فيبوناتشي أن الخالق عز وجل أستعمل هذه النسبه في أظهار جمال مخلوقاته. لذلك نستخدم هذه النسبة لأنها مستخدمه في ما هو أكبر منا.
ـــــــــــــــــــــــــــــــــــــــــــــــــ
من ويكيبيديا
التقسيم الذهبي هو تقسيم لمستقيم بحسب النسبة الذهبية. بحيث يكون الطول الكلي a+b بالنسبة لطول القطعة الأطول a مساوياً للنسبة بين a إلى القطعة الأقصر b.
في الرياضيات، تحقق قيمتان عدديتان النسبة الذهبية إذا كانت النسبة بين مجموع هذين العددين والأكبر منهما تساوي النسبة بين أكبر العددين والأصغر بينهما. وهو عبارة عن ثابت رياضي معرف تبلغ قيمته 1.6180339887 تقريبا.
لو نُظر إلى مستطيلات مختلفة، لوُجد بعضها أجمل من الآخر. وفي معظم الأحيان تكون نسبة أبعاد هذه المستطيلات بعضها إلى بعض هي نفسها. وتسمى هذه المستطيلات "المستطيلات الذهبية" وخارج قسمة طولها على عرضها يسمى "الرقم الذهبي".
طريقة إنشاء المستطيل الذهبي. المربع مبين باللون الأحمر
فنجد أنه في المستطيل الذهبي :
و جرت العادة أن يكتب الرقم الذهبي باعتماد الحرف الاغريقي "فاي" أو
. وقد ظهرت هذه التسمية سنة 1914 وفاء لذكرى "فيدياس"، وهو نحّات قام بتزيين "البارثينون" في أثينا.و يظهر الرقم الذهبي أيضا في أشكال هندسية أخرى منها خماسي الأضلاع المنتظم، وهو شكل هندسي ذو خمس أضلاع ومحتوى في دائرة، وأضلاعه وزواياه كلها متقايسة. وفي هذا الشكل يمثل خارج قسمة القطر على أحد الأضلاع الرقم الذهبي.
ما هي القيمة العددية للرقم الذهبي ؟
قيمة الرقم الذهبي الدقيقة هي
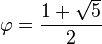كما يمكن إثبات أنّ قيمتها 
أيضا ولإيجاد قيمة تقريبية لهذا الرقم يمكننا استعمال آلة حاسبة. قيمة التقريبية هي 1.618 ولكن عدد الأرقام العشرية لا متناهية ولا يمكن توقّعها أو التكهن بها.و يمكننا أيضا اعتماد متوالية أو "سلسلة فيبوناتشي" للاقتراب من الرقم الذهبي. وقد تم وضع هذه المتوالية في العصر الوسيط على يد عالم الرياضيات الإيطالي ليوناردو دا بيزّا (نسبة إلى بيزّا المدينة الإيطالية) المسمّى "فيبوناتشي"، لدراسة تكاثر الأرانب.
و أول رقمين في هذه السلسلة هما 1. ولإيجاد مختلف عناصرها، نجمع العنصرين السابقين. فنحصل بالتالي على السلسلة التالية :
و بقسمة كل عنصر على سابقه (بداية من الـ1 الثاني)، نقترب شيئا فشيئاً من الرقم الذهبي
و في النهاية، يمكننا اعتماد هذه الصيغة الرياضية لإيجاد قيمة قريبة من قيمة φ :
كيف يمكن الاستفادة من الرقم الذهبي ؟
الرقم الذهبي معروف على الأرجح منذ عصور ما قبل التاريخ. فقد استعمله مهندسون وفنانون كثر منذ العصور القديمة. فهرم "خوفو"، المبني في سنة 2800 ق.م. تقريبا، يظهر أن مهندسه استعمل الرقم الذهبي وكذلك شأن "البارثينون" بأثينا، الذي تم بناؤه في القرن الخامس ق.م وأيضا يوجدفى أهرامات الجيزة بمصر.
و في عصر النهضة، استعمل العديد من الرسّامين (مثل "بييرو ديلاّ فرانشيسكا" أو "ليوناردو دا فينشي") المظاهر الجمالية المرتبطة بالرقم الذهبي في لوحاتهم. وقد أبرز "دا فينشي" كذلك كتابا يبيّن الخصائص الرياضية والجمالية والعجيبة للرقم الذهبي ويسمى هذا الكتاب " "De divina proportio(أو التناسب الإلهي) وقد ألفه كاهن إيطالي اسمه "فرا لوكا باشيولي".
و يظهر الرقم الذهبي كذلك في ميدان الموسيقى ذلك أن صانع الكمانات الإيطالي "أنتونيو ستراديفاري" (و اشتهر "ستراديفاريوس") استخدم هو الآخر هذا الرقم في صنع كماناته الشهيرة مع نهاية القرن السابع عشر للميلاد.
و في القرن العشرين، اهتم العديد من المهندسين والرسامين بالرقم الذهبي في إنجازاتهم، وبالخصوص المهندس الفرنسي "لو كوربيسيي" والرسّام الإسباني "سلفادور دالي",
ويستخدم الرقم الذهبي أيضًا في الأسواق المالية وأسواق العملات والمعادن، بل هو من أهم الأدوات المستخدمة في التحليل الفني لتلك الأسواق؛ فعندما تقوم أسعار الأوراق المالية - أو العملات أو المعادن - بتصحيح مسارها (بمعنى أن تنخفض بعد اتجاه صعودي، أو ترتفع بعد اتجاه هبوطي) يقوم المحللون الفنيون لتلك الأسواق بحساب نسب ارتدادات الأسعار (أي تحديد مدى ذلك الارتفاع أو الانخفاض)، وتلك النسب كلها مشتقة من الرقم الذهبي.
ما هي خصائص الرقم الذهبي ؟
بالإضافة إلى ميزاته الجمالية، فإن الرقم الذهبي يمتاز بخاصية جبريّة مهمّة، إذ أنه يكفي أن تضيف إليه 1 لتجد مربّعه (أي
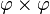). وبعبارة أخرى فإن :
و هذه الصيغة الأخيرة هي الصيغة العامة لتعريف الرقم الذهبي.
و هناك خاصية أخرى تنجرّ عن السابقة وهي أنه يكفي أن ننقص الرقم الذهبي من 1 حتى نجد مقلوبه (أي
) وبالتالي فإن :1 -
أين يمكن إيجاد الرقم الذهبي ؟يظهر الرقم الذهبي في العديد من الإنجازات الإنسانية، ولكن أيضا في الطبيعة بعض الأحيان وبشكل تقريبي مثل:
- الشكل الهندسي لنجم البحر الذي يمتاز بشكل خماسي الأضلاع ارتفاع السرة عن الأرض مساو، هو الآخر، للرقم الذهبي.
- ايضا فان موقع مدينة مكة المكرمة (مدينة مقدسة ) في دولة المملكة العربية السعودية يحقق الرقم الذهبي بالنسبة لمقاييس الكرة الارضية
لمشاهدة الموضوع الأصلي إضغط هنا
المصدر: RSS الحوت السوري
lhid hgksfm hg`ifdm H, Goldin raito ,lh 'vdrm pshfih fhgjwhldl >>